1. Bài toán so khớp - đối sánh mẫu và tầm ứng dụng của nó
Bài toán so khớp - đối sánh mẫu có thể được phát biểu một cách dễ hiểu là việc thực hiện tìm kiếm một chuỗi con xuất hiện hay không trong một đoạn văn bản dài. Nếu chuỗi con đó xuất hiện thì cần chỉ ra vị trí xuất hiện đầu tiên. Đầu vào của bài toán gồm một văn bản T được lưu trong mảng T[1..n] có độ dài n và chuỗi con cần tìm (khuôn mẫu) P được lưu trong P[1..m] có độ dài m, thông thường n >> m; Các phần tử của mảng T và P là các ký tự được rút từ một bảng chữ cái hữu hạn ∑; đầu ra là vị trí đầu tiên tìm thấy P trong T nếu có.
Bài toán so khớp - đối sánh mẫu là một trong những bài toán phổ biến, có tầm ứng dụng rộng rãi, ngoài việc ứng dụng trong việc tìm kiếm chuỗi con trong một đoạn văn bản dài như trên, chúng ta còn thấy được ứng dụng của bài toán so khớp - đối mẫu trong các vấn đề sau:
- Vấn đề xây dựng phần mềm Anti-virus: Bản chất của việc quét, phát hiện và diệt virus chính là vấn đề quét để so khớp mẫu, mẫu cần so khớp (P) chính là mã thực thi của virus, còn T chính là mã thích thi của các file được quét.
- Vấn đề hoạt động của bộ định tuyến gói tin (Routers), tường lửa (firewall/ proxy), hay hệ thống phát hiện xâm nhập (IDS) trong hệ thống mạng: Định tuyến là quá trình tính toán để đưa ra quyết định chặng tiếp theo (next hop) của gói tin bằng cách tìm ra luật áp dụng, tương ứng với tiền tố (trong bảng định tuyến) dài nhất khớp với địa chỉ đích trong header của gói tin. Việc hệ thống tường lừa/proxy hay Hệ thống phát hiện xâm nhập(IDS) đưa ra các quyết định đều dựa trên việc tìm kiếm và áp dụng luật có mức độ khớp tốt nhất với các thông tin hiện tại.
Do là một bài toán kinh điển, đã được đặt ra từ lâu, nên thuật toán giải quyết bài toán này khá phong phú, với các mức độ tối ưu khác nhau. Nhiều thuật toán trong số đó đã được coi là kinh điển, được đem vào giới thiệu trong các giáo trình Cấu trúc dữ liệu và giải thuật. Bài báo này giới thiệu với các bạn một thuật toán giải quyết bài toán dựa vào việc ứng dụng Otomat. Thực tế đây là một thuật toán có giai đoạn tiền xử lý phải thực hiện thủ công (định hình Otomat) nên ít được sử dụng trong thực tế, tuy nhiên tư tưởng giải quyết là giải quyết khá hay.
2. Otomat hữu hạn và ứng dụng của nó trong việc giải quyết bài toán so khớp - đối sánh mẫu
2.1. Otomat và ứng dụng của nó
Các bạn chuyên tin ở bậc Đại học sẽ được học một môn riêng về Otomat và ngôn ngữ hình thức. Ở đây mình chỉ trình bày vắn tắt một số điểm cơ bản:
Định nghĩa: Một Otomat hữu hạn gồm 5 thành phần (Q, qo, A, ∑, δ) trong đó:
• Q là một tập hợp hữu hạn các trạng thái.
• qo ∈ Q là trạng thái đầu.
• A ⊆ Q là một tập hợp đặc biệt của các trạng thái chấp nhận(kết thúc).
• ∑ là một bảng chữ cái đầu vào hữu hạn.
• δ là một hàm từ Q x ∑ -> Q, có tên hàm chuyển tiếp của M (hay còn gọi là tập luật).
Hoạt động của Otomat hữu hạn: Otomat hữu hạn bắt đầu trong trạng thái qo và lần lượt đọc từng ký tự chuỗi đầu vào của nó. Nếu Otomat đang ở trong trạng thái q và đọc từng ký tự đầu vào a, nó dời từ trạng thái hiện hành đến trạng thái mới q’ bằng cách thực hiện hàm chuyển δ với các tham số tương ứng (q’ = δ (q, a)). Nếu trạng thái q hiện tại của Otomat là một trạng thái kết thúc (q ∈ A), thì ta nói Otomat chấp nhận chuỗi được đọc, và quy trình hoạt động của Otomat kết thúc.
Otomat có nhiều ứng dụng trong việc xử lý ngôn ngữ hình thức, ngôn ngữ tự nhiên: hàm δ có thể coi là một tập các quy tắc ngữ pháp của một ngôn ngữ. Ôtômát có thể ứng dụng trong việc phát hiện và nhận dạng ngôn ngữ tự nhiên, trong việc xây dựng các ngôn ngữ lập trình và nhiều ứng dụng khác...
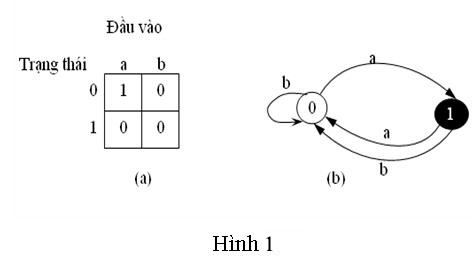
Hình 1 minh họa một Otomat hữu hạn có 2 trạng thái, tập trạng thái Q = {0, 1}, trạng thái bát đầu qo = 0 và bảng chữ cái đầu vào ∑ = {a, b}. Hình (a) biểu diễn bảng giá trị của hàm chuyển tiếp δ. Hình (b) là sơ đồ chuyển tiếp trạng thái. Trạng thái 1 là trạng thái chấp nhận (kết thúc) duy nhất (được tô đen). Các cạnh có hướng biểu diễn các bước chuyển tiếp. Ví dụ về hoạt động của Otomat này: Nếu ta có chuỗi đầu vào là T = abaaa, thì bắt đầu từ trạng thái 0, đọc vào ký tự a, hàm δ(0, a) được thực hiện, chuyển sang trạng thái 1 (δ(0, a) = 1). Vì chuỗi đầu vào chưa kết thúc nên đọc tiếp ký tự b, hàm δ(1, b) = 0, nên trạng thái hiện tại là 0.. Tương tự như thế, khi đọc hết chuỗi T, thì Otomat này đã chuyển qua các trạng thái <0, 1, 0, 1, 0, 1>, và vì kết thúc ở trạng thái 1 (là trạng thái chấp nhận) nên Otomat dừng lại và chấp nhất chuỗi T này.
Việc xác định một Otomat là ta đi xác định 5 thành phần đầu vào ở trên. Vì hoạt động của các Otomat là giống nhau, nên việc lập trình không khó, chỉ khác nhau ở các yếu tố đầu vào, trong đó việc xác định giá trị của hàm chuyển δ là việc quan trọng và khó nhất, do đó có thể nói: Một Otomat có thể được xác định, nếu chúng ta xác định được giá trị của hàm chuyển δ.
2.2. Ứng dụng Otomat để giải quyết bài toán so khớp - đối sánh mẫu
Tư tưởng của phương pháp này gồm 2 bước:
Bước 1: Xây dựng một Otomat hữu hạn tương ứng với mẫu P
Bước 2: Cho Otomat này đọc lần lượt từ ký tự của văn bản T. Trong khi chưa đọc hết T, nếu Otomat đạt đến trạng thái kết thúc, thì dừng lại và thông báo tìm thấy, và ký tự vừa được đọc trước khi kết thúc cũng là ký tự cuối cùng của P, nên ta dễ dàng tìm ra vị trí tìm thấy chuỗi con. Ngược lại, nếu đọc hết P mà Otomat vẫn không thể đạt trạng thái kết thúc thì ta thông báo không tìm thấy P trong T.
Trong 2 bước nêu trên, ta thấy: giả sử bước 1 ta đã thực hiện được, thì bước 2 là bước rất đơn giản: chỉ việc cho Otomat đọc từng ký tự của T, kiểm tra các trạng thái và thông báo. Ta sẽ tập trung quan tâm bước 1, là bước xác định Otomat hữu hạn tương ứng với P. Như đã nói ở trên, để xác định Otomat tương ứng với P, chính là ta đi xác định bảng giá trị của hàm δ ứng với các tham số tương ứng.
Thông thường Otomat hữu hạn tương ứng với mẫu P sẽ có m + 1 trạng thái, tương ứng với một trạng thái bắt đầu (trạng thái 0) và m trạng thái chuyển). Trạng thái m (thứ m +1) là trạng thái kết thúc. Như vậy, khi Otomat này đọc trúng ký tự lần lượt có trong P, nó sẽ chuyển từ trạng thái thứ k sang trạng thái k+1(k = 0 -> m). Trong trường hợp ký tự đọc vào không có trong P, thì tùy tình huống, Otomat sẽ quay về trạng thái 0, hoặc trả về một trạng thái k’, là giá trị của trạng thái thể hiện mức độ khớp của P và T tại thời điểm đang xét. Như vậy giá trị của hàm δ luôn thể hiện mức độ khớp của P và T.
Để dễ hình dung, chúng ta xét ví dụ sau:\
Cho văn bản T = abababacaba và mẫu P = ababaca. Xây dựng Otomat hữu hạn tương ứng với mẫu P. Sử dụng Otomat này để kiểm tra xem mẫu P có xuất hiện trong T hay không? Nếu có thì xuất hiện ở vị trí nào?
Giải quyết:
Bước 1: Xây dựng Otomat tương ứng với P (xác định hàm δ)
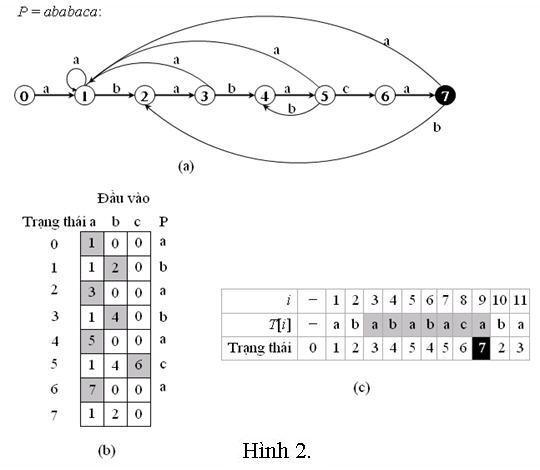
Vì mẫu P có độ dài m = 7, nên Otomat cần xây dựng có 8 trạng thái (trạng thái bắt đầu 0 và trạng thái kết thúc 7). Khi Otomat này đọc ký tự lần lượt có trong P thì chuyển từ trạng thái k sang trạng thái k+1 nên ta có giá trị hàm δ là: δ(0, a) = 1, δ(1, b) = 2, δ(2, a) = 3, δ(3, b) = 4, δ(4, a) = 5, δ(5, c) = 6, δ(6, a) = 7. Còn nếu Otomat đang ở trạng thái 1, mà đọc vào ký tự a (không phải là ký tự tiếp theo của P), thì Otomat phải trả về giá trị trạng thái thể hiện mức độ khớp tốt nhất của P và T là trạng thái 1, (P và T có tiền tố con chung là a, có độ dài 1), do đó δ(1, a) = 1. Còn nếu Otomat đang ở trạng thái 1, mà đọc vào ký tự c (hoặc bất cứ ký tự nào khác a, b), thì Otomat phải trả về giá trị trạng thái 0, vì khi đó P và T không có tiền tố con chung nào, do đó δ(1, c) = 0.
Với lý luận tương tự, ta có thể xác định các giá trị khác của hàm δ. Hình 2 thể hiện bảng giá trị của hàm δ, sơ đồ lưu chuyển cô Otomat này, nhưng không thể hiện ở mức chi tiết: Những trường hợp làm cho trạng thái chuyển về trạng thái bắt đầu không được thể hiện. Quan sát kỹ hình 2 và mẫu P, chúng ta sẽ nắm được cách xác định δ một cách đầy đủ và chính xác.
Bước 2: Cho Otomat này đọc lần lượt từ ký tự của văn bản T, ta thấy Otomat sẽ chuyển qua các trạng thái sau: <0, 1, 2, 3, 4, 5, 4, 5, 6, 7> thì đạt trạng thái kết thúc. Như vậy trong văn bản T có chuỗi P. Vị trí kết thúc của P trong T là vị trí T[9], tương ứng với vị trí bắt đầu là T[3]. Kết luận là ta tìm thấy mẫu P trong văn bản T ở vị trí T[3].
3. Kết luận và đánh giá
Về mặt tư tưởng giải quyết vấn đề, tôi cho rằng đây là một phương pháp hay. Tuy nhiên nếu xét về hiệu quả tính toán thì chưa cao, thể hiện ở: việc xác định các giá trị hàm δ của Otomat tương ứng với một mẫu cho trước phải làm khá thủ công, mặc dù việc lập trình Otomat sau khi xác định δ và thực hiện hiên bước 2 thì khá đơn giản. Mặt khác, nếu tốc độ mỗi lần đọc của Otomat là một ký tự thì tốc độ xử lý khá chậm, còn nếu nhiều hơn một ký tự thì Otomat ta cần xây dựng có tính phức tạp tương đối cao. Tuy nhiên nhận thấy đây, là một tư tưởng hay nên tôi mạnh dạn chia sẻ cùng bạn đọc. Xin trân trọng cảm ơn.
Người viết bài: Nguyễn Tuấn Nghĩa
Trung tâm CNTT